|
|
back |
Defauts
1.5 DEFAUTS DANS LES CRISTAUX
1.5.1 Introduction
Lecristal parfait constitué d'un réseau de Bravais et d'un motif associé est une abstraction. Il sert de référence et permet l'étude de certaines propriétés comme la densité, le comportement élastique ou la chaleur spécifique.
En réalité, tous les milieux cristallins présentent des défauts, qui ne doivent pas a priori être considérés comme nuisibles. Au contraire, des cristaux parfaits seraient le plus souvent dénués de toutes propriétés intéressantes. On ne peut pas fabriquer de transistors avec du silicium parfait (sect. 2.7), il n'est pas possible d'obtenir des aimants permanents à partir de fer parfait ( 3.8.6), etc. La liste de ces exemples pourrait être allongée de manière quasi illimitée, en puisant dans tous les domaines de la science de l'ingénieur.
Il est donc à peine exagéré de dire que les matériaux cristallins sont, avant tout intéressants par leurs défauts. Ces derniers sont classés en quatre catégories, qui font l'objet des paragraphes suivants.
Laprésence de chaque type de défaut peut avoir un effet sur plusieurs propriétés. Cet effet varie d'un matériau à l'autre, c'est pourquoi seules des indications de portée générale seront données à ce sujet dans cette section. Des informations plus précises sont fournies dans les chapitres suivants, lors de l'étude de matériaux définis.
1.5.2 Vibrations thermiques, phonons
L'énergie thermique emmagasinée dans un solide prend essentiellement les formes suivantes:
• mouvement oscillatoire des atomes
• mouvement rotatoire des molécules
• déplacement et excitation des électrons.
Les atomes n'occupent donc pas de façon statique les places qui leur sont réservées dans un cristal, ce qui constitue un premier défaut. A température ambiante, l'amplitude de leur mouvement vibratoire est de l'ordre de 5 à 10% d'une distance interatomique. Une analyse sommaire de ce mouvement est possible à partir de la représentation de l'énergie mise enjeu dans une liaison, donnée au paragraphe 1.3.5. La force de rappel Fr agissant sur l'atome, à une distance Ar de sa position moyenne r0 vaut, d'après (1.36) :
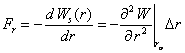(1.61)
Soit a la constante de rappel :
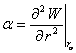(1.62)
L'équation du mouvement de l'atome s'écrit :
(1.63)
où m est la masse de l'atome. Une solution de (1.63) est du type:
(1.64)
La fréquence f du mouvement vaut donc
(1.65)
La constante a est liée au module de compressibilité (1.41) et donc déterminable expérimentalement. Pour des cristaux d'éléments de poids atomiques moyens (Fe, Cu, Ge), on obtient par ce modèle f = 1013 Hz à température ambiante.
Lorsqu'on ne considère pas seulement un atome mais un ensemble d'atomes reliés entre eux, il apparaît que l'état vibratoire de ce réseau est quantifié. Cet état peut être représenté par une somme d'ondes acoustiques de fréquences différentes. Le quantum d'énergie associé à ces ondes s'appelle phonon par analogie au quantum d'énergie associé à une onde électromagnétique, le photon. L'étude du spectre (c'est-à-dire de la distribution en énergie) des phonons d'un cristal constitue l'un des chapitres de la physique du solide [5].
1.5.3 Défauts ponctuels. Définitions
On appelle défauts ponctuels, les défauts se présentant en des points isolés du cristal. Ils sont de plusieurs types, dont les plus importants sont représentés schématiquement à la figure 1.32.
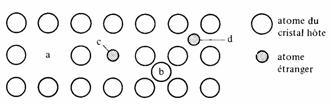
Fig. 1.32 Défauts ponctuels : a, lacune; b, auto-intersticiel; c, atome étranger en substitution; d, atome étranger intersticiel.
On appelle lacune le défaut consistant en l'absence d'atome dans un site qui devrait normalement en contenir un. Tous les cristaux contiennent des lacunes, sans
cesse produites et supprimées par l'agitation thermique. Le nombre volumique n des lacunes varie en fonction de la température selon la loi
(1.66)
oùN est le nombre volumique des sites devant contenir des atomes et Wl une énergie dite de formation des lacunes. Dans l'aluminium par exemple, Wl = 0,75 eV.
Lorsqu'un atome du cristal occupe une position normalement vide, il constitue un défaut appelé auto-intersticiel. La densité des auto-intersticiel est nettement plus faible que celles des lacunes.
La présence d'atomes étrangers, en position de substitution ou en position intersticielle, constitue un défaut dont les incidences sur la conductivité sont utilisées dans la technique des semi-conducteurs ( 2.7.2 et 2.7.3).
D'autres types de défauts ponctuels existent dans les cristaux ioniques.
1.5.4 Dislocations. Définitions
Les dislocations sont des défauts dans l'arrangement des atomes, présentant une allure filiforme. Leur comportement détermine dans une très large mesure les propriéés mécaniques des métaux. Il existe deux types de dislocations, la dislocation coin et la dislocation vis.
Les dislocations apparaissent et se déplacent dans les cristaux (fig. 1.33), lorsque des contraintes appliquées provoquent une déformation plastique (sect. 6.3).
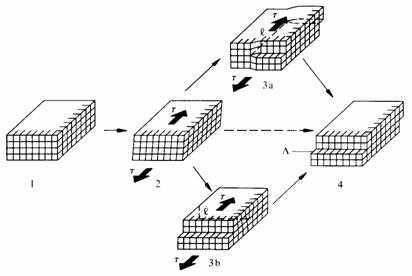
Fig. 1.33
Au stade 1, le cristal est libre de toute contrainte. Soumis progressivement à une contrainte tangentielle τ, il présente tout d'abord une déformation élastique (réversible) correspondant au stade 2. Si τ augmente encore, le cristal finira par subir la déformation permanente représentée au stade 4. Celle-ci résulte d'un glissement des atomes dans un plan Λ.
On pourrait imaginer que ce glissement se produit brutalement, tous les liens de valence cédant simultanément pour se reformer immédiatement, après une translation de la partie supérieure du cristal par rapport à la partie inférieure. En fait, la contrainte de cisaillement minimum τo nécessaire pour obtenir une déformation permanente selon ce processus serait beaucoup plus grande ( 1.5.5) que celle déterminée par l'expérience. Cela démontre qu'en réalité le mécanisme envisagé ne se produit pas.
Au contraire, la déformation permanente se constitue progressivement, en passant par les stades intermédiaires 3a ou 3b. De cette façon, l'énergie mécanique mise en jeu est beaucoup plus faible, car seule une petite région du cristal est déformée à la fois.
La dislocation est repérée par la ligne l, tracée dans la zone du cristal la plus déformée. La figure 1.33 montre que l peut prendre deux orientations extrêmes.
La dislocation apparaissant au stade 3a est appelée dislocation vis. Elle possède la caractéristique d'être orientée parallèlement à τ, et de se déplacer perpendiculairement à t.
La dislocation apparaissant au stade 3b est appelée dislocation coin. Elle possède la caractéristique d'être orientée perpendiculairement à τ et de se déplacer parallèlement à τ.
On remarque que les deux types de dislocations conduisent à la même déformation finale.
D'un point à un autre, une ligne de dislocation peut passer progressivement du type coin au type vis, et réciproquement (fig. 1.34).
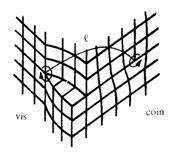
Fig. 1.34
1.5.5 Calcul de τo
On suppose, pour simplifier le calcul, que la déformation est concentrée entre deux plans réticulaires voisins (fig. 1.35).
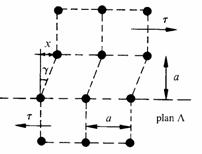
Fig. 1.34
L'énergie W nécessaire par unité de surface dans A, pour obtenir un déplacement x, s'exprime en première approximation par une relation du type:
(1.67)
où Wo est une constante. Or :
(1.68)
Par définition ( 6.2.3) du module de cisaillement G,
(1.69)
d'où
(1.70)
Cette évaluation très simple de τo donne un résultat trop élevé. Un calcul plus élaboré montre que τo = G/30. Malgré cette correction la valeur théorique reste, comme annoncé dans le paragraphe précédent, largement supérieure aux valeurs expérimentales. On relève couramment dans les métaux des valeurs de τo comprises entre 10-5 G et 10-4G.
1.5.6 Vecteur de Burgers
Le vecteur de Burgers b caractérise les dislocations. Son orientation indique le sens dans lequel les atomes se sont déplacés, son module mesure l'importance de ce déplacement.
Le vecteur de Burgers est déterminé par la procédure représentée à la figure 1.36 pour le cas d'une dislocation coin.
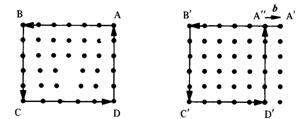
Fig. 1.36
On décrit un circuit fermé ABCDA dans un plan perpendiculaire à l ,en empruntant le sens trigonométrique direct. Ce circuit doit être assez éloigné de l pour se trouver dans une zone de cristal peu déformée. On compte en partant de A le nombre de noeuds rencontrés sur chaque tronçon rectiligne AB, BC, CD, DA.
Sur la base de ces comptages on effectue un trajet homologue A'B'C'D'A" dans un cristal parfait.
Le vecteur de Burgers est défini comme le vecteur de fermeture b = A" A'
Le vecteur de Burgers reste constant sur toute la longueur d'une dislocation.
1.5.7 Calcul de l'énergie d'unedislocation
Le calcul de l'énergie de déformation associée à une dislocation est un développement utile car il fournit plusieurs renseignements intéressants concernant le comportement des dislocations et la déformation plastique en général.
On assimile, pour ce calcul, le cristal à un milieu continu et l'on choisit le cas d'une dislocation vis. Dans ces conditions, le calcul de l'énergie de la dislocation est ramené à celui de l'énergie de cisaillement emmagasinée dans une couronne cylindrique entourant la dislocation. Cette couronne est représentée à la figure 1.37, en place à gauche, sous forme développée à droite.
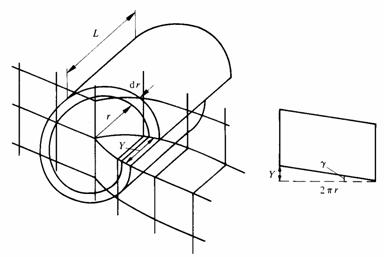
Fig. 1.37
L'énergie spécifique de déformation au cisaillement est donnée, lorsque l'angle de cisaillement x varie de 0 à 7, par la relation générale:
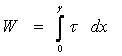(1.71)
En tenant compte de la définition ( 6.2.3) du module de cisaillement G on obtient:
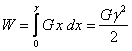(1.72)
L'énergie de déformation dans la couronne cylindrique d'épaisseur dr vaut donc :
(1.73)
L est la longueur de la dislocation.
Finalement, l'énergie de la dislocation est donnée par :
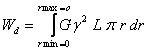(1.74)
Trois approximations permettent de calculer cette intégrale de manière simple sans changer la nature du résultat final.
Premièrement on remplace la limite inférieure d'intégration rmin = 0 par rmin = a, où a est le module d'un vecteur fondamental du réseau cubique simple dans lequel s'est développé la dislocation. Cela revient à négliger l'énergie de déformation dans un petit volume seulement. Comme le module du vecteur de Burgers b est égal à a, il est équivalent de poser rmin = b.
Deuxièmement on choisit rmax = b exp (4π) ≅ 3 ⋅ 105 b. Cela revient à considérer que la distorsion du réseau devient négligeable à une distance d'environ 300 000 intervalles inter-atomiques.
Troisièmement, on admet que γ = b/2πr entre rmin et rmax.
Sous ces conditions (1.74) devient :
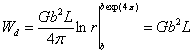(1.75)
Cette expression montre que l'énergie dedéformation associée à la dislocation est
proportionnelle à b 2. Or, le vecteur de Burgers est toujours orienté dans le sens de la déformation par cisaillement. Il est donc plus facile de déformer un cristal selon les directions dans lesquelles les atomes se trouvent à la distance minimum les uns des autres.
proportionnelle à la longueur de la dislocation. Celle-ci tendra donc à être rectiligne à moins qu'elle ne soit fermée sur elle-même. Dans ce cas, son périmètre aura tendance à diminuer.
proportionnelle au module de cisaillement. Comme G croît avec le module d'élasticité EY( 6.2.2) cela traduit simplement le fait (évident) qu'il faut davantage d'énergie pour déformer plastiquement un matériau à haut module d'élasticité.
Les procédés utilisables pour diminuer la mobilité des dislocations et par conséquent augmenter la limite élastique des matériaux sont étudiés au paragraphe 6.3.6.
1.5.8 Joint de grains
Entre les grains ( 1.4.1) constituant un polycristal existe une fine zone de raccordement dans laquelle les atomes possèdent une énergie de liaison, en valeur absolue inférieure à celle des atomes situés à l'intérieur des grains. Cette zone, appelée joint de grains constitue un défaut bidimensionnel.
Divers phénomènes peuvent se produire dans les joints de grains. Ils influencent les propriétés des matériaux polycristallins. On mentionnera en particulier :
la ségrégation d'impuretés, c'est-à-dire l'accumulation de celles-ci dans les joints de grains. La ségrégation se produit dans un intervalle de températures déterminé. Si la température est trop élevée, les impuretés demeurent en solution solide ( 5.2.2), si au contraire la température est trop basse, la mobilité des impuretés est insuffisante pour leur permettre d'atteindre le joint de grains. La ségrégation produit des effets de fragilité et de corrosion intergranulaires.
la nucléation, c'est-à-dire l'apparition d'une nouvelle phase (sect. 5.2) se produit généralement dans les joints de grains.
la diffusion d'atomes à partir de la surface de l'échantillon, qui est plus rapide dans les joints de grains qu'ailleurs. Cette diffusion peut également être responsable de fragilité et de corrosion intergranulaires.
La fracture par glissement relatif de deux faces d'un joint de grains.
le blocage des dislocations, qui ne peuvent traverser un joint de grains en raison du désalignement des vecteurs fondamentaux des deux grains voisins.
La taille des grains a tendance à augmenter avec le temps, principalement dans les matériaux purs où le réarrangement des atomes sur les faces des joints de grains n'est pas gêné par la présence d'atomes étrangers. Lorsqu'il atteint de grandes proportions, ce phénomène dégrade les qualités mécaniques. La rapidité de la croissance dépend fortement de la température.
Les grains d'un polycristal sont décrits par leur taille, leur forme et leur orientation. Plusieurs normes définissent la manière de mesurer ces caractéristiques.